2022. 5. 9. 13:18ㆍ개발하다가
이슈
평면 상의 간단한 충돌 알고리즘을 구현한다면, 선분과 선분의 위치 관계와 평면상 원과 선분의 위치 관계 정도가 대표적으로 필요할 겁니다. 겉보기에는 높아 봐야 고등학생 수준 알고리즘이고 실제로도 그렇습니다. 한국어로 치면 거의 안 나오지만 영어로 치면 많이 나오기는 하는데요, 뭔가 불만이 있다면 코드가 조금 오래 걸려 보인다는 거라든지 유도를 읽기 귀찮다는 거겠죠. 사실 후자가 큽니다.
* 이 글은 고민하는 과정이 들어 있지, 정답 같은 걸 담고 있지 않습니다. 그래서 사실 오답을 담고 있을 수도 있습니다.
문제 1. 동일 평면상 원과 선분의 위치 관계
한국어로 구글에 '원과 선분의 교점'이라고 치면 이상하게 원과 직선의 교점이란 제목의 글들만 나옵니다. 아무튼, 보통 이렇게 4개의 입력이 주어질 겁니다.

대충 방법은 이렇게 되겠습니다.
1. 선분 PQ에서 C에 가장 가까운 점을 찾는다
2. 그 점과 C 사이의 거리가 r 이하일 경우 원과 선분은 만나거나 선분이 원 안에 있다
충돌이라는 유스케이스 관점에서 볼 때, 선분이 원 안에 있다는 것과 선분과 원에 교점이 있다는 말은 경우에 따라 구분할 필요가 없을 수도 있습니다.
- 원 안으로 선분이 들어가지 않았으면 좋겠는 경우: 이 경우를 위해 알고리즘을 쓴다면, 선분 상에서 원의 중심으로부터 가장 가까운 점을 구하여 비교해야 합니다. 가장 가까운 점이 안쪽으로 들어가지 않아야 합니다.
- 원 안에서 선분이 나가지도 않고 원 안으로 선분이 들어가지도 않았으면 좋겠는 경우: 이 경우를 위해 이 알고리즘을 쓴다면, 선분 상에서 원의 중심으로부터 가장 가까운 점과 먼 점 모두를 구하여 비교해야 합니다. 가장 가까운 점과 가장 먼 점이 원 안과 밖에 있는 여부가 같아야 합니다.
가장 가까운 점을 찾는 방법은 2가지입니다만, 따지고 보면 같은 방법입니다.
- 직선 벡터방정식을 미분하여 극소점을 찾기(직선은 무한히 뻗어나갈 수 있어 극대점이 있을 리가 없으니 미분계수가 0이기만 하면 됩니다.)
- 정사영을 구하여 선분 상에서 그와 가장 가까운 점을 찾기
왜 같냐고요? 별들에게 물어보세요. 수학이 원래 그렇습니다.
직선 벡터 방정식은 이렇습니다.
L: P1 + (Q1-P1)t
선분의 경우 t는 [0,1] 범위여야 합니다.Q1-P1=V(vx, vy)라고 하겠습니다. 이때 선분 상 점에 대하여 중심과의 거리를 D라고 하면 다음이 성립합니다.

t에 대한 변화율은 다음과 같습니다.

이 값이 0일 조건은 단순히 선형방정식을 풀면 되고, 정리하면 다음과 같습니다.

t가 [0,1] 범위 안에 없으면 가장 가까운 점은 t=0이거나 t=1일 때입니다. (이차함수니까)
이후에는 단순히 위치 벡터 P1+vt와 C의 거리를 구하면 됩니다.
cf) 정사영으로 과정을 거치자면 이렇습니다.


마찬가지로 t가 [0,1] 범위 안에 없으면 가장 가까운 점은 t=0이거나 t=1일 때입니다. C++에서 이를 구현해 볼까요?
bool intersect(const vec2& center, float r, const vec2& p1, const vec2& q1){
#ifdef 미분
vec2 pc(center-p1);
vec2 pq(q1-p1);
float t=pc.dot(pq)/pq.dot(pq);
t=clamp(t,0,1);
return (p1+pq*t).distance2(center) <= r*r;
#else
vec2 pc(center-p1);
vec2 pq(q1-p1);
vec2 proj=pq.dot(pc)*pq.normal();
float t=(proj[0]-p1[0])/pq[0];
t=clamp(t,0,1);
return (p1+pq*t).distance2(center) <= r*r;
#endif
}제가 보기에는 미분 버전이 부동소수점 / 연산이 적으니(normal()에 하나 숨겨져 있음) 더 빠른 것 같습니다.
그런데 이걸로 괜찮은 게 맞을까요? 정작 교점을 모르지 않나요? 유스케이스를 다시 떠올려 봅시다.
- 원 안으로 선분이 들어가지 않았으면 좋겠는 경우: 이 경우를 위해 알고리즘을 쓴다면, 선분 상에서 원의 중심으로부터 가장 가까운 점을 구하여 비교해야 합니다. 가장 가까운 점이 안쪽으로 들어가지 않아야 합니다. 60fps 정도를 상정해 봅시다. 아주 까다로울 필요는 없는 경우 촘촘한 검사 덕분에 교점을 P1+t(Q1-P1) 하나라고 가정해도 됩니다. (실근이 2개인 경우, P1+t(Q1-P1)은 그 둘의 중점입니다.) 교점이 작용점이므로 t값을 자르지 않고 리턴하여 사용할 수 있어 보입니다.
- 원 안에서 선분이 나가지도 않고 원 안으로 선분이 들어가지도 않았으면 좋겠는 경우: 이 경우를 위해 이 알고리즘을 쓴다면, 선분 상에서 원의 중심으로부터 가장 가까운 점과 먼 점 모두를 구하여 비교해야 합니다. 가장 가까운 점과 가장 먼 점이 원 안과 밖에 있는 여부가 같아야 합니다. 이런 알고리즘이 필요하다면, 기존에 원 외부에 있던 선분에 대한 작용점은 t가 [0,1] 범위 안에서 어떤 식으로 될지 모르고 기존에 원 내부에 있던 선분에 대한 작용점은 t가 0,1 중 하나입니다. '만들어라' 한다면 보통 선분의 양 끝점이 둘 다 원 안에 있거나 밖에 있는지를 먼저 조사하고 밖에 있으면 위를 비롯한 알고리즘으로 이어지는 코드를 만들면 쉽겠지만 조건문이 마음에 들지 않는다면, t에 대한 이차방정식을 풀어야죠. 제가 단위 함수 내에서 조건을 나누는 것을 굉장히 싫어합니다.
이 알고리즘은 공간 상 선분과 구의 관계로 그대로 확장될 수 있습니다. 벡터 차원수만 늘리면 됩니다.
문제 2. 동일 평면상 두 선분 간의 위치 관계
이 알고리즘이 유명하기는 한 모양입니다만 경우가 너무 많아서 싫습니다. 게다가 교점 자체를 찾아 주지도 않습니다. 조금 다른 방식을 떠올려 봅시다. 직접 소개는 안 하지만, 이 알고리즘도 고려해 보세요.

선분 하나는 그대로 두고 나머지 한 선분에서는 아무 거나 한 점을 선택해 봅시다. 이때, 둘 간의 교점이 있기 위한 선분 P의 다른 끝점 P2의 위치는 다음 그림과 같습니다.

선형대수를 배운 적이 있다면 뭔가 떠오를 수도 있습니다. 벡터 Q1-P1, Q2-P1를 가지고 표준 평면의 좌표들을 표현하면(기저 변환) 다음과 같은 그림이 탄생합니다.

이는 부등식 3개 x≥0, y≥0, x+y≥1에 해당합니다. 기저 변환은 Q1-P1, Q2-P1을 열벡터로 하는 2x2 행렬의 역행렬을 곱하여 할 수 있습니다. P2는 입력으로 주어졌을 테니, P2-P1에 그 변환 행렬을 곱해 주고 결과 좌표에 저 3개를 적용하면 됩니다.
하지만 2개의 이슈가 남았습니다.
- 그래서 교점은?
- P1이 Q 혹은 Q의 연장선 상에 있는 경우(이 경우 역행렬이 없습니다.)
교점은 보통의 경우 변환된 P2의 좌표를 (a,b)라고 할 때, P의 맥락에서 쉽게 표현될 수 있습니다. (a+b)는 P1`(변환 후 원점)과 P2`사이의 값은 P1`(원점)과의 거리에 정비례하게 증가합니다. 말하기도 부끄럽습니다. 그래서 교점은 P1+(P2-P1)t (t=1/(a+b)) 겠군요. 충돌 맥락 기준으로는, P2, Q1, Q2 중 하나일 겁니다. 역행렬이 있는 경우라면요. 그러니까 2번째 이슈를 함께 이야기하지 않을 수 없습니다. 충돌 맥락에서 보면 직사각형 2개의 변이 맞닿아 있는 경우도 굉장히 흔할 겁니다.
P1이 Q 상에 있는 경우를 알아보려면 P1-Q1, P1-Q2를 내적한 결과가 P1-Q1, P1-Q2의 길이의 합과 부호만 다른지 확인하면 됩니다(부호까지 같으면 연장선 상에 있는 겁니다). 이 경우에는 P1을 작용점으로 할 수도 있지만, 토크를 도입했고 P와 Q가 나란하고 긴 경우라면 오차가 제법 생길 수 있습니다.
역행렬이 없다면 억지로 만드는 것은 어떨까요? 예시를 통해 확인해 봅시다.
P1(0,0), P2(1,1), Q1(2,3), Q2(4,6)
이 경우 P1은 Q의 연장선 상에 있으니, 행렬 [[2, 4], [3, 6]]은 역행렬이 없습니다. 역행렬이 없는 행렬에 대하여 아주 조금의 수치를 조정하여 역행렬을 있게 만들면 아주 먼 곳에 근이 하나 생길 겁니다. 역행렬이 없는 행렬에 대하여 항상 역행렬을 억지로 붙일 수 있는 방법은 다음과 같습니다.

이 작은 상수를 편의상 0.001이라고 하면 역행렬은 다음과 같습니다.

이를 통해 P2를 이동시키면 [250.093, -124.859]이며, y값이 음수이므로 교점은 없습니다. 엡실론 값을 점점 0에 가깝게 하여 직접 계산해 보시면 이 계산의 의미가 조금 더 명확해질 겁니다. 원본 행렬에 변화가 조금 밖에 없으므로, 실질적으로는 그냥 행렬식으로 나누는 과정만 뺀 겁니다.
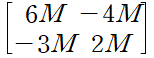
(M은 절댓값이 매우 큰 음/양의 실수)이런 변환이 있다고 가정하고 적용하면 [2M, -M]으로 부호가 다르니 대놓고 교점이 없다고 생각할 수 있습니다. 다른 경우를 확인해 봅시다.
P1(0,0), P2(1,1), Q1(-1,0), Q2(1,0)
같은 방식으로 역행렬을 구하면 다음과 같습니다. 이 변환을 적용하면 [-M, -M]입니다. 위 그림을 따라가자면 교점이 있을 수도 있고 없을 수도 있습니다. 이런 경우라면, P1만 교점으로 보면 됩니다. 기하학적으로 생각하면, 선분 Q를 아주 약간 치웠을 때 치우는 방향에 따라 교점이 있을 수도 있고 없을 수도 있는 것이므로 아주 약간의 움직임으로 P1이 선분 Q의 한쪽 방향에 있거나 다른 쪽 방향에 있게 된다는 말입니다.

P1(0,0), P2(2,4), Q1(1,2), Q2(3,6)같은 방식으로 역행렬을 구하면 다음과 같고, 변환을 적용하면 [0,0]입니다. 이런 경우라면 두 선분이 한 직선 상에 있다는 말은 되지만, 겹치는지는 모릅니다.

이를 역행렬이 있는 것을 포함하여 일반화하면 이렇게 됩니다.
1. Q1-P1, Q2-P1을 구한다.
2. 그것을 열벡터로 하는 것의 수반 행렬(adjugate, 2x2 행렬의 수반 행렬은 1행 1열과 2행 2열을 바꾸고 나머지는 부호를 바꾼 것)과 행렬식을 구한다.
3-1. 행렬식이 0인 경우 수반 행렬에 P2-P1을 곱하고 부호가 다르면 교점이 없고 부호가 같으면 P1이 교점, 둘 다 0이면 특정 좌표에 대하여 대소 비교
3-2. 행렬식이 0이 아닌 경우 역행렬에 P2-P1을 곱한 결과의 성분이 양수이고 그 합 S가 1 이상이면 P1+(P2-P1)/S가 교점
경우가 많아서 싫다고 해 놓고 많이 갈라진 느낌인데, 이는 교점을 알아야 했기 때문입니다. 단순히 분기가 적었으면 좋겠다면, 처음부터 P1과 P2가 Q 및 연장선 위에 있는지 확인하고 없으면 기저 변환 하면 그만입니다.
vec2 segIntersect(const vec2& p1, const vec2& p2, const vec2& q1, const vec2& q2){
vec2 b1(p1-q1);
vec2 b2(p2-q1);
vec2 q(q2-q1);
mat2 adj(
b2[1], -b2[0],
-b1[1], b1[0]
);
float d=adj.det(); // cross2(b1,b2)와 동일. (cross2는 외적의 z좌표)
if(d==0){
vec2 st=adj*q;
if(st[0]*st[1]>0) return q1;
else{
// x 혹은 y좌표만 비교해서,
// p1,p2>q1,q2 혹은 q1,q2>p1,p2인 경우 return NAN;
// 그 외의 경우(등호가 있는 경우도 포함) return 가운데 2개의 중점;
// 대표적으로 태그를 붙여 안정 정렬을 하는 방법이 있습니다.
}
}
else{
vec2 st=adj*q/d;
if(st[0]>=0 && st[1]>=0 && st[0]+st[1]>=1.0f)
return q1+q/(st[0]+st[1]);
return NAN;
}
}
나눗셈은 정수나 부동소수점이나 기계 명령상 sqrt만큼이나 오래 걸리는 계산입니다. 조금만 더 축약해 봅시다.
2. 수반 행렬과 행렬식을 구한다.
3. 행렬식은 0보다 크거나 0보다 작거나 0인데,
- 수반 행렬에 P2-P1을 곱한 것을 st (2차원 벡터)라고 할 때 0보다 큰 경우나 작은 경우나,
(st[0] <= 0 && st[1] <= 0 && st[0]+st[1] <= D) || (st[0] >= 0 && st[1] >= 0 && st[0]+st[1] >= D)
이것을 다음과 같이 축약할 수 있습니다.
st[0] * st[1] >= 0 && abs(st[0] + st[1]) >= abs(D)
앞 조건을 통과하면 뒤 조건은 절댓값만 맞으면 인정입니다. D != 0인 경우에는 교점이 다음과 같습니다.
P1 + (P2-P1)/((st[0]+st[1]) * D)
D = 0인 경우라도 근이 있으려면 st[0] * st[1] >= 0은 통과해야 함이 위에 증명되어 있습니다. D = 0이라면 당연히 오른쪽 조건도 자동으로 통과합니다. 그럼 남은 처리해야 할 것은 곱한 결과가 [0,0]이 되는 하나뿐입니다.
vec2 segIntersect(const vec2& p1, const vec2& p2, const vec2& q1, const vec2& q2){
vec2 b1(p1-q1);
vec2 b2(p2-q1);
float dt=b1.dot(b2);
vec2 q(q2-q1);
mat2 adj(
b2[1], -b2[0],
-b1[1], b1[0]
);
float d=adj.det(); // cross2(b1,b2)와 동일. (cross2는 외적의 z좌표)
if(st[0] * st[1] >= 0 && abs(st[0]+st[1]) >= abs(d)){
if(st[0] * st[1] > 0) {
return d==0 ? q1 : q1+q/((st[0]+st[1])*d);
}
else{
// x 혹은 y좌표만 비교해서,
// p1,p2>q1,q2 혹은 q1,q2>p1,p2인 경우 return NAN;
// 그 외의 경우(등호가 있는 경우도 포함) return 가운데 2개의 중점;
// 대표적으로 태그를 붙여 안정 정렬을 하는 방법이 있습니다.
}
}
else{
return NAN;
}
}분기 수는 거기서 거기지만, 나눗셈 하나를 곱셈으로 바꾸었습니다.
이 방식은 차원수가 올라가도 사용이 가능한데, 아무래도 역행렬이 아닌 방법으로 선형계를 푸는 것이 귀찮을 겁니다. 다만, 차원수가 올라가면 그만큼 선분끼리 만날 일이 없습니다. 다음을 참고하는 것도 고려할 수 있습니다. wolframalpha를 이용하여 만든 3차원 상의 평면 기저에 대한 유사역행렬 함수입니다. 이 경우 고려 사항이 하나 더 추가되는데, 애초에 4개 점이 동일 평면 상에 있지 않으면 끝점 중 하나에서 만나거나 안 만나거나입니다. 이를 먼저 계산하지 않으면 결과가 잘못될 수 있습니다.
inline mat2x3 pseudoInverse(const mat3x2& m) {
const float& a = m[0][0], & b = m[0][1], & c = m[1][0], & d = m[1][1], & e = m[2][0], & f = m[2][1];
float dd = b * (c * (b * c - a * d) + e * (b * e - a * f)) + a * (a * d * d + a * f * f - b * c * d - b * e * f) + (d * e - c * f) * (d * e - c * f);
mat2x3 ret;
if (dd != 0) {
dd = 1 / dd;
ret[0][0] = d * d * a + f * f * a - d * b * c - f * b * e;
ret[0][1] = -b * a * d + b * b * c + f * f * c - f * d * e;
ret[0][2] = -b * a * f + b * b * e - d * c * f + d * d * e;
ret[1][0] = -c * a * d - e * a * f + c * c * b + e * e * b;
ret[1][1] = -a * b * c + a * a * d - e * c * f + e * e * d;
ret[1][2] = -a * b * e + a * a * f - c * d * e + c * c * f;
mulAll(ret[0], dd, 6);
}
return ret;
}이상으로 마칩니다. 좋은 방법이 많이 있으면 좋겠네요.
'개발하다가' 카테고리의 다른 글
| GPT가 나보다 낫네요? (0) | 2023.03.05 |
|---|---|
| C++에서 템플릿 메타프로그래밍하다가 발생한 오류 (0) | 2022.05.31 |
| 오버플로 없는 short int x 분수 (0) | 2022.05.25 |
| 1초당 목표 위치에 99% 다가가는 카메라 (0) | 2022.05.22 |
| 원 모양 물체의 2차원 비탄성 충돌에 대한 고민 (0) | 2022.05.10 |